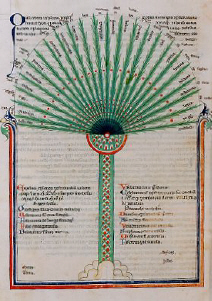
5. Para hacer más claro este argumento, apelamos a la multiplicidad de rayos provenientes de un centro único. Y, así, queremos llevar a concebir cómo surgió la multiplicidad. Conviene advertir para ello que toda la multiplicidad de que se habla ha sido engendrada de una vez, en tanto podremos imaginar en un círculo rayos separados y que realmente no existan; porque se trata aquí de una superficie.
Nada allí de superficie ni de intervalo. Las potencias y las esencias no poseen dimensiones y diríase que todas ellas semejan centros que se reúnen en uno solo. Un ejemplo nos lo ofrecen los rayos que aparecen limitados por la parte de su centro, donde todo converge en la unidad. Sí os hacéis de nuevo con ellos, incluso los rayos que dejaron su centro quedarán sujetos a él, y, ciertamente, tampoco cada uno de los centros se verá separado del centro único y primero. Todos se dan en el mismo lugar y son en tan gran número como los rayos a los que sirven de límite. Y es así como se establece una correspondencia entre los rayos y los centros que se nos muestran, pero, sin embargo, todos ellos constituyen una unidad.
He aquí que si comparamos todos los inteligibles con esos múltiples centros que se refieren y se unen al centro único, su multiplicidad se manifiesta por los rayos mismos, pero sin que sean esos rayos los que la engendran sino los que la dan a conocer. Los rayos, pues, nos servirán en la presente ocasión para ofrecer analógicamente las cosas a las que alcanza la naturaleza inteligible; de este modo se hará presente su multiplicidad y su presencia en todo lugar.